Subscribe
×

Preference: Administration and Health Services

2

Aiming for the truth: understanding the difference between validity and precision

In teaching generations of registrars, a recurring theme is the conflation of the concepts of validity and precision, resulting in an erroneous understanding of the role of statistics. In this article, we clarify the definition of these two concepts, looking at what drives these measures and how they can be maximised.

Understanding error

Clinical epidemiology is the science of distinguishing the signal from the noise in health and medical research. The signal is the true causal effect of a factor on an outcome; for example, a risk factor on a disease outcome or a medication on disease progression. The noise is the variation in the data, which has traditionally been referred to as error.

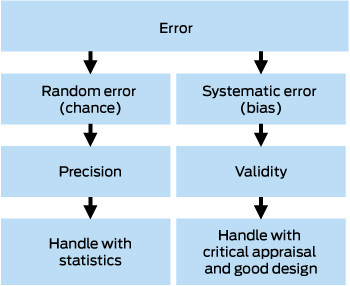
There are two types of errors: random error, also called chance or non-differential error, and systematic error, also known as differential error or bias (Box 1). Random error is the scatter in the data, which statistics uses to estimate the central or most representative point, along with some plausible range, known as the confidence interval. Increasing the sample size shrinks the confidence interval so that we have greater precision in our estimate. However, no statistical test can tell us how close that estimate is to the truth, which is a matter of validity — also known as study validity, to distinguish it from measurement validity or accuracy. Study validity can only be judged by critical appraisal of the design.

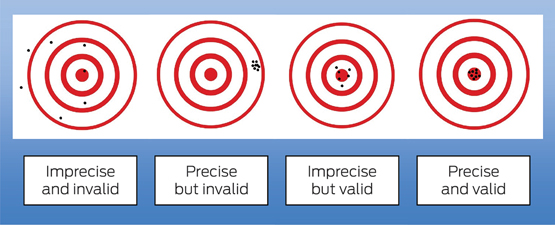
In the widely used Robin Hood analogy of precision and validity (Box 2), Robin Hood represents the researcher, and aiming the bow and arrow at the target represents the study that seeks to find the truth about some cause and effect in medicine. Each arrow fired at the target is the study results and is launched by a bow, which represents the study design. The scatter where the arrows hit the target represents the random error. Statistics can be used to analyse the random error and estimate the most representative point (ie, the effect size of the association under investigation) with its confidence interval. However, statistics do not tell us how far that estimate is from the truth (the bullseye). Systematic error (bias) in the design can be visualised as a warp in the bow (the study design), which causes the arrows to systematically hit off target, missing the bullseye. No matter how many arrows are fired (ie, large sample size) and how precise the estimate is, the estimate is still no closer to the truth.

Validity also has two components: internal validity, which is how accurate or close to the truth the result is; and external validity or generalisability, which is how applicable the result is to the population that the study is investigating.

These concepts, when understood correctly, are very powerful and can lead to some revelations:

  • large sample sizes do not ensure validity;

  • P values do not provide information about the design of a study or the validity of the result;

  • complex statistical models will not necessarily remove bias;

  • critical appraisal skills are the only way to judge validity;

  • small studies can be closer to the truth than large studies if designed better; and

  • study results may be internally valid but not generalisable.

Understanding bias

Epidemiology provides a framework to understand how a design can be biased. Since Sackett1 published his classic article naming 35 different kinds of bias, various authors have updated the list and one recent review listed 74 individual biases.2 All these biases can be classified into three main categories,2 although their use is not always consistent:3

  • selection bias, which is a warp in the way participants are identified or recruited;

  • measurement bias, which is a warp in how information is measured or collected; and

  • confounding, which is a warp in the measure of association or conclusion about causation, due to improper or incomplete analysis.

Selection bias

In general, the process by which study participants are identified or recruited will affect the external validity (generalisability) of the study, but not the internal validity. For example, a study that targets people with dementia by advertising through local media will attract those with less severe dementia (spectrum bias) or with an interest in their health and who are therefore healthier (volunteer bias). Although the results of the study may be true (internally valid) for this group of people with dementia, they may not be applicable to the wider population with more severe dementia (externally invalid).

In some cases, however, selection bias may severely affect the internal validity of the trial. Recruitment via advertising through local media excludes those who have died (survivor bias). If we are exploring the link between smoking and dementia, those who participate in the study may be selectively depleted of smokers, who are likely to die of many other causes before recruitment (eg, heart attack, stroke, chronic obstructive pulmonary disease, cancer). This may then lead to a situation where smokers are under-represented in the dementia group compared with the control population. The study would then erroneously indicate that smoking is protective for dementia, as was published in a 1991 article.4 A prospective study, which avoided survivor bias, subsequently showed the correct result: that smoking increases the risk of dementia.5

Berkson’s bias6 is another example of how selection bias can influence internal validity. In a study of the association between obesity and dementia, one might choose to identify people with dementia from hospital records. Apart from selecting those with more severe dementia, this might also create a spurious association with obesity, given that those with obesity are more likely to end up in hospital because of other health problems compared with those with dementia and no obesity.

Measurement bias

A warp may occur in how the measurements are made, whether these are measurements of the exposure of interest, the outcome of interest or another variable that could be adjusted in the analysis. This source of error will always affect internal validity and hence external validity. In the study investigating the association of smoking and dementia, we can contemplate how we measure smoking (exposure) and dementia (outcome). It is possible that participants with dementia systematically under-report their smoking due to their memory problems (recall bias), which will lead to an underestimate of the true effect or even a reversal. Alternately, a systematic bias that overcalls vascular dementia in smokers (eg, making smoking or vascular disease part of the definition of the outcome) may overstate an association with smoking where there is none in reality.

Analytical bias or confounding

Confounding is a warp in the measure of association or conclusion about causation due to improper or incomplete analysis. A confounder is a variable (or set of related variables) associated with the exposure of interest and the outcome of interest, which causes a spurious or distorted estimate of this association, without being an intermediate between the two. Whereas selection and measurement bias are handled by good design and choice of measures, confounding differs in that, if it is measured accurately, it can be handled in the analysis. As an example, in the study of the association between smoking and dementia, we can postulate a third variable, drinking alcohol, that goes hand in hand with smoking and which may actually be responsible for causing dementia. If this variable (alcohol) is not measured and included in the analysis, the effect of alcohol and smoking on dementia will be inseparable and the effect size will be falsely attributed entirely to smoking. It is in fact possible that smoking does not contribute at all to the risk of dementia but that confounding makes it appear to have an effect, or that smoking has an effect but this is overestimated or underestimated by alcohol. A future article in this series will be devoted to confounding, including relevant information on study design, measuring potentially confounding variables and adjusting for them in the analysis.

Handling selection and measurement bias

The possibilities of selection bias and measurement bias must be anticipated during the planning phase of a study. A good study design will minimise these biases to the point where they are tolerable, that is, unlikely to alter our findings to a clinically meaningful extent. When reading a study, one must make a judgement about the magnitude and direction of the bias. If the bias is likely to be towards the null, meaning that the effect size is smaller in magnitude than it is in reality, then this should be taken into account when interpreting the results. If the study shows an effect despite this bias, then the real effect must be larger and robust. If the bias is likely to be away from the null — meaning that the study will overstate the effect size — then one must be wary of the result.

Conclusion

Differentiating the concepts of validity and precision will help clinicians understand the role of statistics and the importance of critical appraisal when reading articles.

Box 1 –
Random error (chance) is a matter of precision and it is best handled with statistics. Systematic error (bias) is a matter of validity and it is best handled by critical appraisal and good design

Box 2 –
The Robin Hood analogy of precision and validity

Adapted from: Barry C. Accuracy vs precision: what’s the difference? State College: The Minitab Blog; 2012. http://blog.minitab.com/blog/real-world-quality-improvement/accuracy-vs-precision-whats-the-difference (accessed Sept 2016).

Targeted health research funding — submit your ideas

The National Health and Medical Research Council (NHMRC) has created an online pathway for community and professional groups to submit their ideas for targeted health research funding.

The pathway allows the submission of proposals throughout the year. All eligible proposals will undergo review and prioritisation biannually, and recommendations will be provided to the NHMRC Research Committee for consideration.

Ideas should focus on research that has the potential to improve health outcomes for the community, reduce the burden of disease on the health system and Australian economy, and contribute to the global research effort.

The online pathway is part of NHMRC’s revised framework for identifying and prioritising targeted calls for research (TCRs). It is one of several channels for identifying possible TCRs under the new framework, which establishes a set of principles for priority-driven research and provides NHMRC with a mechanism to respond to emerging research needs.

A TCR is a one-time request for grant applications to address a specific health problem. They complement NHMRC’s existing suite of funding schemes by funding research in defined areas of need and when urgent research needs emerge.

A TCR can help stimulate research in a particular area of health and medical science that will benefit Australians. It could be the “tipping point” for a research breakthrough within a disease area — that small injection of targeted funding that will result in changed policy or practice, or a new discovery.

A TCR is typically allocated between $2.5 million and $5 million (depending on the type of research required) from a previously allocated research fund in the NHMRC Medical Research Endowment Account. The number of TCRs awarded each year depends on available funds.

More information on how to make a submission is available on the NHMRC website.

[Comment] Implementation and aspiration gaps: whose view counts?

The Lancet’s Maternal Health Series1–6 paints a sobering picture of the state of maternal health today. The Series focuses on the “mismatch between burden and coverage”, which “exposes a crucial gap in quality of care”6 and spotlights the millions of pregnant women and adolescents who never get access to services at all. But 30 years after the start of the safe motherhood initiative, this mismatch exposes something else as well: a dangerous disconnect between the way the global health community has framed problems, proposed strategies, and pushed solutions, and the lived experience of people and providers.

Upsurge in doctors under billing scrutiny

A doctor has been ordered to repay Medicare rebates worth almost $1.14 million as part of an upsurge in cases of over-billing being investigated by health authorities.

The Professional Services Review has reported a near doubling of the number of cases referred to it by the Health Department as the conduct of medical practitioners, particularly in the preparation of chronic disease management plans and those working in large practices, comes under increased scrutiny.

In its 2015-16 annual report, the PSR said it had received 80 referrals from the Department, a 29 per cent jump from the previous year and an 82 per cent surge from 2013-14.

Of 49 investigations completed last year, 24 resulted in no further action being taken, while 18 were resolved with a negotiated agreement including the repayment of $1.63 million and the partial disqualification of 12 practitioners.

But in seven instances doctors were reprimanded and ordered to repay Medicare benefits worth between $48,380 and $1.138 million. In one instance, a doctor was disqualified from practising for three months.

In all, doctors were ordered to reimburse Medicare almost $4.6 million.

While the vast majority of the 85,000 practitioners providing Medicare reimbursed services are considered to be doing the right thing, the PSR reported several instances of high billing, including a GP who provided 20,000 services in a single year, as well as almost 600 GP Management Plans, 400 Team Care Arrangements and more than 1000 item 2713 mental health services – each of which has a minimum 20-minute time requirement.

A chronic problem

The agency, which is asked to investigate cases that the Health Department cannot resolve or explain, said the use of Chronic Disease Management (CDM) and Health Assessment items was of particular concern.

“Many practitioners who provide high numbers of these services use computer-generated templates; a plan may have minimal content specific to the patient for whom the plan has been prepared,” it said. “Plans sometimes have very generic health advice of the most minimal nature, and sometimes irrelevant to any condition listed in the patient’s clinical record.”

The PSR said that in other instances some GPs were preparing GP Management Plans every 12 months, and reviewing them every three months, without even consulting the patient.

“In some cases, there was little evidence that patients were aware that they had a GP Management Plan, and the precise regularity of reviews every three months…appeared contrived to maximise income rather than being based on clinical assessment.”

A matter of size

The PSR raised concern about the operation of larger medical practices where GPs are engaged as independent contractors who pay the operator a service fee. It said that under current arrangements individual practitioners were held solely accountable for inappropriate billing and the reimbursement of rebates – practice owners retained their share of Medicare rebates.

Local knowledge

The agency warned that overseas-trained doctors were more susceptible to breaching Medicare rules than their local counterparts, accounting for almost 54 per cent of cases referred to it last financial year.

In one instance, it found an “older English graduate…engaged in particularly egregious use” of CDM items, claiming the MBS items 721 and 723 more than 400 times in 12 months, at $240 a time.

Three other international medical graduates were found to have breached the so-called 80/20 rule, which meant they billed 80 or more GP attendance items on 20 or more days in the year. Typically, this would mean providing between 17,000 and 20,000 services attracting a gross rebate of between $800,000 and $1 million.

In all, five practitioners were investigated by the PSR for breaching the 80/20 rule, while a further 15 were identified to have provided more the 60 attendances on more than 100 days.

In mitigation, many explained that they worked very long hours, they knew their patients well so could serve them quickly, that the practice was under-staffed or that they were unaware of the 80/20 rule.

Round-the-clock

The PSR flagged that while some doctors were billing CDM items inappropriately, others had come under suspicion over their provision of urgent after-hours care.

It said that although those referred for investigation had generally satisfied the definition of providing after-hours care, their interpretation of what constituted the need for urgent care was dubious.

“Examination of clinical records has shown that some practitioners have billed these items for medical conditions such as an uncomplicated rash, reissuing prescriptions for…regular medication and for routine completion of medication charts in residential aged care facilities,” the PSR said, adding that the difference in fee between urgent and non-urgent after-hours MBS items was substantial enough to have a significant financial impact on Medicare.

The agency warned that the Government’s review of the MBS and Medicare compliance measures was likely to include ways to use the billing system to “better detect and define possible inappropriate practice”.

The Federal Government has begun work on upgrading the Medicare payments system, inviting private sector upgrade proposals, though it has insisted the system and the information it collects will remain completely in public hands.

Latest news

Pioneering digital disruption: Australia’s first integrated digital tertiary hospital

Digital transformation has started in Australian hospitals

Digital technology now underpins most industries; however, the health care sector (particularly in hospitals) has been slow to transform from traditional paper-based systems of care. In the United States, for example, federal legislation and financial incentives have facilitated the implementation of electronic medical records (EMRs);1 but there are only a handful of advanced EMRs in hospitals outside the US.2 The roll-out of a digital hospital includes an EMR system and other technical components, such as integrated digital vital sign monitoring and digital electrocardiogram (ECG) records. This transformation prompts revolutionary change in the way health care is delivered and monitored.

The enthusiasm for digital transformation in health has been tempered by previous failures, such as some of the unsuccessful EMR installations in the National Health Service in the United Kingdom.3 Digital health care in Australia is well established in primary care and private specialist settings, but so far it has been chequered and controversial in hospital settings, with several independent reviews previously commissioned by government and other bodies.4

There are known adverse consequences and costs accompanying digital transformation of a hospital. These can include poor physician morale, increased frustration and reduced efficiency of care — particularly in the emergency department (ED) and outpatient setting.5,6 Previous EMRs have also struggled to support traditional clinical workflows, with the American College of Physicians calling for EMRs to support the cognitive flow of physicians.7

However, there are many benefits to the installation of an EMR system, which include more efficient and effective care, clinical decision support and a reduction in adverse events.8,9 There is no doubt that digital health care is the future. We describe here the challenging digital transformation of the Princess Alexandra Hospital (PAH) into the first integrated digital tertiary hospital in Australia.

Digital transformation

PAH was chosen as the exemplar site for a statewide EMR program and to become Australia’s first tertiary digital hospital. It is an adult teaching hospital that delivers quaternary level care to a diverse, high acuity patient cohort. PAH has 6529 staff members, 833 overnight beds and cares for over half a million outpatients a year. The aim was to build an integrated digital hospital which provided care across the emergency, inpatient and outpatient settings. Vital sign monitoring and ECGs are digitised and delivered to the EMR via Wi-Fi for immediate viewing. Medications are the only significant component not included in this implementation and are planned for early 2017.

After an 18-month pre-implementation stage, the digital transformation of PAH was achieved using a big bang approach, with digital conversion occurring rapidly over 2 weeks.

Clinician concerns and experiences

It was a challenge to transform such a large, diverse organisation with a myriad of highly specialised workflows and a high acuity workload. The clinicians at our hospital had several valid concerns, the clear articulation of which influenced the course of the project.

Clinicians have had a difficult relationship with information technology (IT) projects — as evidenced by the problems affecting the Queensland health payroll.10 It became clear that a traditional IT-led approach to the digital transformation of a large tertiary hospital was unlikely to be successful. Practising clinicians — rather than IT staff with clinical backgrounds — joined the leadership team to ensure that the project remained patient and staff centred. Clinicians had to drive the project rather than act as consultants. This clinical leadership enhanced the meaningful articulation of the potential long term benefits of an EMR — particularly, the promise of a rich database of clinical information that could be used to improve the care provided.

In addition, a large amount of training was required over a short period of time. Clinicians were concerned about the adequacy of the project-prescribed training and its logistics while maintaining the existing hospital function. The preparation involved 32 000 hours of training for 5384 staff. Traditional IT project-delivered web-based training alone was inadequate. Therefore, additional training, such as dress rehearsals using mock patients in clinical settings with the new technology, was organised to practise scenarios such as deteriorating patients and outpatient workflows before digitisation. This level of engagement with training required a brief reduction in elective surgical and outpatient activity.

Clinicians were concerned that the digital transformation would slow their work speed and that it would remove existing specialised ways of undertaking complex care delivery. We customised the software to enable practice across a variety of hospital settings, from a brief fracture clinic appointment to a lengthy geriatric assessment. The executive and senior clinicians, who balanced this disruption against the long term clinical benefits, articulated an acceptance that care would be temporarily slower and less efficient.

Concerns about patient safety during the digital transformation have been one of the barriers to EMR implementation.11 The EMR roll-out at PAH on a large and rapid scale involved a series of potential risks for our patients, including possible suboptimal design of the off the shelf systems causing errors of omission and commission;7 difficult integration of systems leading to errors from delays or lost information; the learning curve of the practitioners using the system; numerous changes to clinical workflows; and loss of patient focus, as attention was also directed to new technology.

In order to deal with these concerns, a patient safety team, independent of the digital hospital project, was deployed to create a patient safety watch to monitor for adverse events across a suite of pre-determined patient outcomes. The patient safety watch consisted of three components:

  • patient safety officers, who were clinicians deployed on the IT help desk — on a 24 hours a day basis — to monitor calls and to escalate patient safety concerns that could be hidden among the technical problems reported by staff

  • patient safety rounds, which consisted of senior clinicians walking the hospital over the initial 2-week period to assess if there were any unreported patient safety concerns; and

  • patient safety data dashboard, where a dashboard, which monitored several indicators, including calls to deteriorating patients and cardiac arrest rates, was deployed with the roll-out. The mortality rate was also closely monitored.

During the initial 2-week period, the patient safety watch reported to the hospital executive implementation committee twice daily to ensure that there was strong clinical governance and that the roll-out was safe to continue and risks were being managed appropriately. It was this clinical endorsement that then allowed the IT team to progress to the next step of the roll-out. This clear, independent focus on patient safety outcomes contributed to clinician engagement and reduced anxiety.

Patient outcomes during digitisation

Although adverse events continued to occur, we did not detect any significant harm directly attributable to the digital transformation. We have monitored patient outcomes closely for the 6 months post roll-out and, when compared with the same time period the previous year to help account for seasonal variation, we found no significant difference in the number of rapid response team calls to deteriorating patients or cardiac arrests (Appendix). There were numerous anecdotes suggesting that we could expect a spike in mortality associated with a large EMR roll-out. Although there is not yet enough data for a statistically robust mortality analysis, no such mortality spike was observed (Box).

Challenges of the EMR roll-out

There still needs to be a completion of the clinical workflows with electronic prescribing. A major source of technical challenges relates to the interfaces between the new system and legacy systems, such as the patient administration system, some of which have been in service for more than 30 years.

There was a widespread disruption of normal workflows. Efficiency in the ED was reduced, with an initial 25% increase in average ED length of stay. After 6 weeks, this had begun to improve with a return to baseline at 6 months. There has been a slowing of procedural efficiency (eg, operating theatres), which continues to improve as optimisation of the software and workflows occurs. Outpatient workflow was also disrupted for some particularly large complex clinics with many new patients, such as the oncology clinic.

Retrieving meaningful clinical data for large groups of patients from our system is more challenging than expected. Significant clinical input is required to build data definitions and to extract clinically appropriate information.

Benefits of the EMR roll-out

Patient records are now readily available throughout the hospital. The digital recording of all ECGs and vital signs within the hospital has improved visibility of this information. Support for decision making has been deployed in areas such as identifying deteriorating patients. Laborious paper chart audits to record patient outcomes have been previously involved in hospital quality improvement projects. However, the digital hospital has the potential to provide readily available data to improve the quality and efficiency of care.

Data from the EMR will be collated to provide rich clinical information to facilitate system improvements. We have started by developing a digital dashboard that reports the details of calls to deteriorating patients in the hospital. These data enable visibility of our operations and patient outcomes in this critical area.

Lessons learnt

Establishing Australia’s first tertiary digital hospital was a difficult task. Strong executive and clinical leadership was essential. Disrupted workflows and reporting structures still require refinement; nevertheless, very few staff members have expressed a wish to return to paper.

Disrupted workflows will become more efficient; however, a true return on this significant investment will be delivered when the data collected can be used to improve the quality and efficiency of health care delivery. Some data are already being provided for clinical and operational improvement, but a mature, easily accessible database will take years to establish.

Because the digital transformation of a hospital is a clinical event, patient outcomes, rather than IT project goals, need to remain the focus. Clinical leadership is essential for this process.

Box –
Inpatient mortality before and after digital hospital implementation

Family doctors need help to tackle domestic violence

Family doctors are more likely than police to see the results of family and domestic violence, and have a key role to play in early intervention and treatment, the AMA says in an updated Position Statement.

AMA President, Dr Michael Gannon, said the trusted role of the family doctor gave GPs a clear insight into the damage caused by the violence.

“Two women are killed nearly every week in Australia due to family and domestic violence,” Dr Gannon said.

“The health effects of family and domestic violence in both the immediate victims and their families are devastating, and it is not only women who are the victims.

“Women experiencing domestic violence will share their experiences with their GPs more often than with any other professional group, and the health impacts persist long after the violence ceases.”

Women who have experienced domestic or family violence have higher levels of mental and physical disorders, higher rates of suicide attempts, and are more likely to have an impaired quality of life than other women.

“Children who grow up witnessing and experiencing domestic violence can also be profoundly affected.”

Related: Violence screening “complex”

The AMA is committed to providing important information and guidance to empower doctors, particularly GPs, to provide better support for victims.

The release of the revised and updated Position Statement on Family and Domestic Violence 2016 this week coincided with a major meeting of Commonwealth, State, and Territory ministers at the COAG National Summit on Reducing Violence Against Women and their Children.

It calls on all Australian governments to properly fund and resource specialised family and domestic violence support services, including housing and crisis accommodation.

“Family violence affects people of all genders, sexualities, ages, socio-economic background, and cultures,” Dr Gannon said.

“And we are now also seeing increasing instances of elder abuse, with grandmothers and grandfathers, many frail and vulnerable, being subjected to violence from family members.

“Men can be victims. Women can be perpetrators. But it is clear that the overwhelming majority of people who experience such violence are women.”

Stamping out family and domestic violence requires commitment and coordination from governments; support services; the related professions, especially medical, health and legal; neighbourhoods; and families – backed by adequate funding.

The Women’s Electoral Lobby (WEL) backed the AMA’s call for funding, saying it was disappointing that crisis services for women and children escaping violence were not on the agenda for the COAG Summit in Brisbane.

“The Summit plans to hold roundtable discussions on such topics as ‘using behavioural insights to reduce domestic violence’ and ‘innovative uses of technology’, as well as important discussions on the Family Court, Indigenous insights and experiences, and the effects of domestic violence on children, but there is nothing on the agenda about crisis services, including women’s refuges,” WEL said in a statement.

“WEL calls on the COAG Summit to include support for long-term, secure Commonwealth-State funding for women’s crisis services in its deliberation and follow-up actions.”

Latest news

 

Radiotherapy in Australia: report on the second year of a pilot collection 2014–15

In this report on the second pilot year collection of national radiotherapy data, data were received from 66 out of 74 service locations across Australia. These services contributed information on over 56,400 courses of radiotherapy delivered in 2014–15.For non-emergency treatment, 50% of patients started treatment within 10 days and 90% started within 28 days. For those who needed emergency treatment, 91% began treatment within the emergency timeframe.

[Review] Doctors in China: improving quality through modernisation of residency education

There is growing recognition that the ultimate success of China’s ambitious health reform (enacted in 2009) and higher education reform (1998) depends on well educated health professionals who have the clinical, ethical, and human competencies necessary for the provision of quality services. In this Review, we describe and analyse graduate education of doctors in China by discussing the country’s health workforce and their clinical residency education. China has launched a new system called the 5 + 3 (5 year undergraduate and 3 year residency [standardised residency training]), which aims to set national quality standards.

Whistleblower doctors exempt from jail threat

Doctors will no longer be threatened with imprisonment for speaking out about conditions in immigration detention after the Federal Government amended its controversial Australian Border Force Act.

Immigration Department Secretary Michael Pezzullo has confirmed that provisions of the Act have been changed so that secrecy and disclosure rules that threaten whistleblowers with up to two years’ imprisonment no longer apply to health professionals including doctors, nurses, psychologists, pharmacists and dentists.

The backdown follows outcry by the AMA and many other medical groups and individuals against the Act’s secrecy provisions, including the launch of a High Court challenge by the group Doctors for Refugees and the Fitzroy Legal Service.

Doctors for Refugees President Dr Barri Phatafod told the Guardian the decision was a “huge win for doctors and recognition that our code of ethics is paramount”.

The provisions make it a criminal offence for those contracted to provide services to the Department of Immigration and Border Protection to record or disclose information obtained in the course of their work. The penalty is up to two years’ imprisonment.

The operation of immigration detention centres, especially those located offshore on Nauru and Manus Island, has been surrounded by controversy amid claims of assault, self-harm, child abuse and substandard living conditions and medical services.

Groups including Amnesty International have condemned the detention regime, claiming it is causing enormous harm to the wellbeing of asylum seekers and refugees, particularly children.

The AMA has for several years called for the establishment of an independent medical panel empowered to investigate and report on detention centre conditions directly to Parliament.

Doctors have protested that the secrecy provisions in the ABF Act conflict with their ethical duties and their obligations under the Medical Board of Australia’s Code of Conduct, most particularly their paramount obligation to the health of their patients.

These concerns have been magnified by a number of cases in which, it is claimed, authorities have sought to intervene in or override clinical advice on the transfer of detainees in need of medical attention, including the death of Omid Masoumali, who was medically evacuated to Australia from Nauru more than 24 hours after setting himself alight.

The Government denied the intention of the law was to prevent doctors from speaking up on behalf of their patients, and earlier this year Immigration Minister Peter Dutton said he thought it unlikely that health practitioners would be prosecuted under the Act.

But it was revealed that Dr Peter Young, who oversaw the mental health care of detainees for three years, was the subject of Australian Federal Police investigation, including access to his electronic communications and at its most recent National Conference, the AMA passed an urgency motion asking the Federal Council to “look into the matter” of AFP surveillance of doctors.

Dr Young told the Guardian the Government made the amendment because it wanted to avoid legal scrutiny of its policy.

“It’s a big backdown from the Government, and they’ve made it because they didn’t want to go to court, they knew they were going to lose, and they didn’t want their planning and policies discoverable in an open court. That’s what it’s about,” he said.

Adrian Rollins